Analytic diffusion¶
examples/analytic_diffusion.py models a diffusion process and reports the error from the model integration by comparison to the analytic solution (intial concentrations are taken from Green’s function expressions for respective geometry).
$ python analytic_diffusion.py --help
usage: analytic_diffusion.py [-h] [-D D] [--t0 T0] [--tend TEND] [--x0 X0]
[--xend XEND] [--mu MU] [-N N] [--nt NT]
[-g GEOM] [--logt] [--logy] [--logx] [--random]
[-k K] [--nstencil NSTENCIL] [--linterpol]
[--rinterpol] [--num-jacobian] [--method METHOD]
[-p] [-a ATOL] [--rtol RTOL] [-e]
[--random-seed RANDOM_SEED] [-s SAVEFIG] [-v]
optional arguments:
-h, --help show this help message and exit
-D D, --D D 0.002
--t0 T0 3.0
--tend TEND 7.0
--x0 X0 0.0
--xend XEND 1.0
--mu MU -
-N N, --N N 64
--nt NT 42
-g GEOM, --geom GEOM u'f'
--logt False
--logy False
--logx False
--random False
-k K, --k K 0.0
--nstencil NSTENCIL 3
--linterpol False
--rinterpol False
--num-jacobian False
--method METHOD u'bdf'
-p, --plot False
-a ATOL, --atol ATOL 1e-06
--rtol RTOL 1e-06
-e, --efield False
--random-seed RANDOM_SEED
42
-s SAVEFIG, --savefig SAVEFIG
u'None'
-v, --verbose False
$ python analytic_diffusion.py --plot --efield --mu 0.5 --nstencil 5 --k 0.1 --geom f
$ python analytic_diffusion.py --x0 0 --xend 1000 --N 1000 --mu 500 -D 400 --nstencil 3
Note -D 475
$ python analytic_diffusion.py --x0 0 --xend 1000 --N 1000 --mu 500 -D 475 --nstencil 7
Still problematic (should not need to be):
$ python analytic_diffusion.py --plot --nstencil 5 --logy --D 0.0005
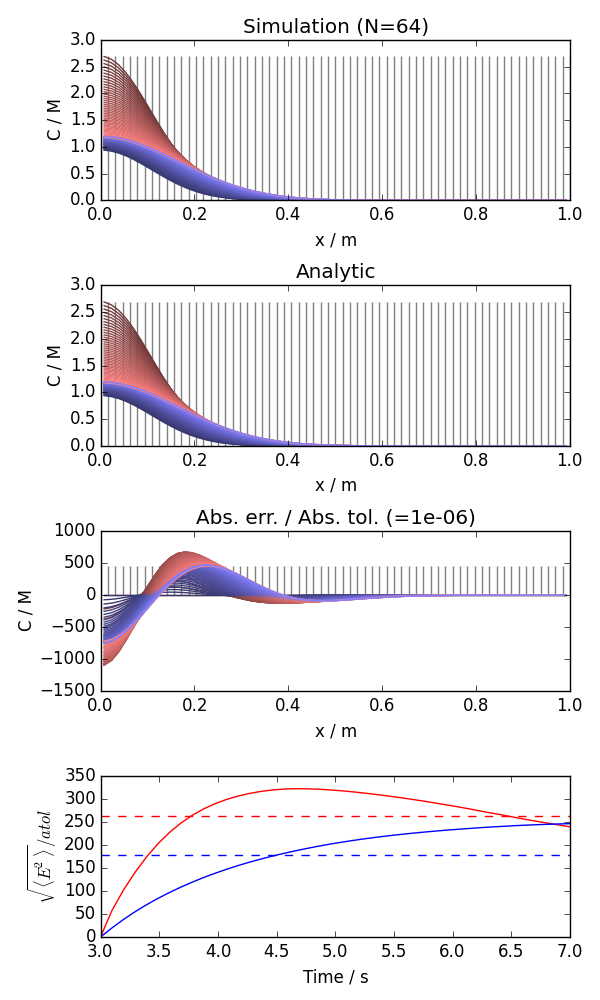
Here is an example generated by:
$ python analytic_diffusion.py --plot --nstencil 3 --k 0.1 --geom f --savefig analytic_diffusion.png
- analytic_diffusion.cylindrical_analytic(x, t, D, mu, x0, xend, v, logy=False, logx=False)[source]¶
Evaluates the Green’s function:
\[c(x, t) = \frac{x_{end}-x_{0}}{4 \pi D t} \ e^{-\frac{(x - \mu - vt)^2}{4Dt}}\]which satisfies:
\[\frac{\partial c(x, t)}{\partial t} = D\nabla^2 \ c(x, t) - \vec{v} \cdot c(x, t)\]where \(\nabla\) in cylindrical coordinates with axial symmetry is:
\[\nabla = \frac{1}{x}\]and where \(\nabla^2\) is:
\[\nabla^2 = \frac{1}{x} \frac{\partial}{\partial x} \left( x \frac{\partial}{\partial x} \right)\]
- analytic_diffusion.flat_analytic(x, t, D, mu, x0, xend, v, logy=False, logx=False)[source]¶
Evaluates the Green’s function:
\[c(x, t) = \frac{x_{end}-x_{0}}{\sqrt{4 \pi D t}} \ e^{-\frac{(x - \mu - vt)^2}{4Dt}}\]which satisfies:
\[\frac{\partial c(x, t)}{\partial t} = D\nabla^2 \ c(x, t) - \vec{v} \cdot c(x, t)\]where \(\nabla\) in cartesian coordinates with planar (yz-plane) symmetry is:
\[\nabla = \frac{\partial}{\partial x}\]and where \(\nabla^2\) :
\[\nabla^2 = \frac{\partial^2}{\partial x^2}\]
- analytic_diffusion.integrate_rd(D=0.002, t0=3.0, tend=7.0, x0=0.0, xend=1.0, mu=None, N=64, nt=42, geom=u'f', logt=False, logy=False, logx=False, random=False, k=0.0, nstencil=3, linterpol=False, rinterpol=False, num_jacobian=False, method=u'bdf', plot=False, atol=1e-06, rtol=1e-06, efield=False, random_seed=42, savefig=u'None', verbose=False)[source]¶
- analytic_diffusion.spherical_analytic(x, t, D, mu, x0, xend, v, logy=False, logx=False)[source]¶
Evaluates the Green’s function:
\[c(x, t) = \frac{x_{end}-x_{0}}{\sqrt{4 \pi D t^3}} \ e^{-\frac{(x - \mu - vt)^2}{4Dt}}\]which satisfies:
\[\frac{\partial c(x, t)}{\partial t} = D\nabla^2 c(x, t) - \vec{v} \cdot c(x, t)\]where \(\nabla\) in spherical coordinates for a isotropic system is:
\[\nabla = \frac{\partial}{\partial x}\]and where \(\nabla^2\) is:
\[\nabla^2 = \frac{1}{x^2} \frac{\partial}{\partial x} \left( x^2 \frac{\partial}{\partial x} \right)\]